7. Polar Coordinates

Exercises

    a. Polar Coordinate System

  1. Convert the rectangular coordinates (x,y)(x,y) into polar coordinates (r,θ)(r,\theta):

    1. (x,y)=(3,3)(x,y)=(3,3)

      Hint

      The relations between rectangular coordinates (x,y)(x,y), the polar coordinates (r,θ)(r,\theta) are x=rcos⁡θr=x2+y2y=rsin⁡θtan⁡θ=yx\begin{array}{ll} x=r\cos\theta\qquad \qquad &r=\sqrt{x^2+y^2} \\ y=r\sin\theta&\tan\theta=\dfrac{y}{x} \end{array}

      [×]

      Answer

      (r,θ)=(32,π4)(r,\theta)=\left(3\sqrt{2}, \dfrac{\pi}{4}\right)

      [×]

      Solution

      Since the point is (x,y)=(3,3)(x,y)=(3,3) which is in the 1st1^\text{st} quadrant, we have: r=x2+y2=9+9=2⋅9=32θ=arctan⁡(yx)=arctan⁡(33)=π4\begin{aligned} r&=\sqrt{x^2+y^2}=\sqrt{9+9}=\sqrt{2\cdot9}=3\sqrt{2} \\ \theta&=\arctan\left(\dfrac{y}{x}\right) =\arctan\left(\dfrac{3}{3}\right) =\dfrac{\pi}{4} \end{aligned} So the point is: (r,θ)=(32,π4) (r,\theta)=\left(3\sqrt{2},\dfrac{\pi}{4}\right)

      js 

      [×]

    2. (x,y)=(−2,−23)(x,y)=(-2,-2\sqrt{3})

      Hint

      Be careful to check the quadrant.

      [×]

      Answer

      (r,θ)=(4,4π3)(r,\theta)=\left(4,\dfrac{4\pi}{3}\right)

      [×]

      Solution

      Since the point is (x,y)=(−2,−23)(x,y)=(-2,-2\sqrt{3}), we have: r=x2+y2=4+12=4 r=\sqrt{x^2+y^2}=\sqrt{4+12}=4 Notice that (x,y)=(−2,−23)(x,y)=(-2,-2\sqrt{3}) is in quadrant III. So to find θ\theta, we add π\pi radians to the arctan⁡\arctan: θ=arctan⁡(yx)+π=arctan⁡(−23−2)+π=π3+π=4π3\begin{aligned} \theta&=\arctan\left(\dfrac{y}{x}\right)+\pi =\arctan\left(\dfrac{-2\sqrt{3}}{-2}\right)+\pi\\ &=\dfrac{\pi}{3}+\pi=\dfrac{4\pi}{3} \end{aligned} So the point is: (r,θ)=(4,4π3) (r,\theta)=\left(4,\dfrac{4\pi}{3}\right)

      js 

      [×]

    3. (x,y)=(−2,5)(x,y)=(-2,5)

      Hint

      Be careful to check the quadrant.

      [×]

      Answer

      (r,θ)=(29,arctan⁡(5−2)+π)≈(5.385,1.95rad)≈(5.385,111.8∘)\begin{aligned} (r,\theta)&=\left(\sqrt{29},\arctan\left(\dfrac{5}{-2}\right)+\pi\right) \\ &\approx(5.385,1.95\,\text{rad}) \approx(5.385,111.8^\circ) \end{aligned}

      [×]

      Solution

      Since the point is (x,y)=(−2,5)(x,y)=(-2,5), we have: r=x2+y2=4+25=29≈5.385\begin{aligned} r&=\sqrt{x^2+y^2}=\sqrt{4+25}=\sqrt{29} \\ &\approx5.385 \end{aligned} Notice that (x,y)=(−2,5)(x,y)=(-2,5) is in quadrant II. So to find θ\theta, we add π\pi radians to the arctan⁡\arctan: θ=arctan⁡(yx)+π=arctan⁡(5−2)+π≈1.95rad\begin{aligned} \theta&=\arctan\left(\dfrac{y}{x}\right)+\pi =\arctan\left(\dfrac{5}{-2}\right)+\pi\\ &\approx 1.95\,\text{rad} \end{aligned} In degrees we have: θ≈1.95rad×180∘πrad≈112∘\begin{aligned} \theta&\approx1.95\,\text{rad} \times\dfrac{180^\circ}{\pi\,\text{rad}} \\ &\approx112^\circ \end{aligned} So the point is: (r,θ)=(29,arctan⁡(5−2)+π)≈(5.385,1.95rad)≈(5.385,112∘)\begin{aligned} (r,\theta)&=\left(\sqrt{29},\arctan\left(\dfrac{5}{-2}\right)+\pi\right) \\ &\approx(5.385,1.95\,\text{rad}) \approx(5.385,112^\circ) \end{aligned}

      js 

      [×]

    4. (x,y)=(12,32)(x,y)=\left(\dfrac{1}{2},\dfrac{\sqrt{3}}{2}\right)

      Answer

      (r,θ)=(1,π3)(r,\theta)=\left(1,\dfrac{\pi}{3}\right)

      [×]

      Solution

      We compute: r=x2+y2=(12)2+(32)2=14+34=1\begin{aligned} r&=\sqrt{x^2+y^2} =\sqrt{\left(\dfrac{1}{2}\right)^2+\left(\dfrac{\sqrt{3}}{2}\right)^2} \\ &=\sqrt{\dfrac{1}{4}+\dfrac{3}{4}}=1\\ \end{aligned} Since both xx and yy are both positive, we know that PP is in quadrant II and thus we compute: θ=arctan⁡(3212)=arctan⁡(3)=π3\begin{aligned} \theta&=\arctan\left(\dfrac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}\right) \\ &=\arctan(\sqrt{3}) \\ &=\dfrac{\pi}{3} \end{aligned} So the point is: (r,θ)=(1,π3) (r,\theta)=\left(1,\dfrac{\pi}{3}\right)

      js 

      [×]
  2. Convert the polar coordinates (r,θ)(r,\theta) into rectangular coordinates (x,y)(x,y):

    1. (r,θ)=(4,π3)(r,\theta)=\left(4,\dfrac{\pi}{3}\right)

      Hint

      The relations between rectangular coordinates (x,y)(x,y), the polar coordinates (r,θ)(r,\theta) are x=rcos⁡θr=x2+y2y=rsin⁡θtan⁡θ=yx\begin{array}{ll} x=r\cos\theta \qquad \qquad &r=\sqrt{x^2+y^2} \\ y=r\sin\theta&\tan\theta=\dfrac{y}{x} \end{array}

      [×]

      Answer

      (x,y)=(2,23)(x,y)=(2,2\sqrt{3})

      [×]

      Solution

      Using r=4r=4 and θ=π3\theta=\dfrac{\pi}{3}, we compute x=rcos⁡θ=4cos⁡(π3)=4⋅12=2y=rsin⁡θ=4sin⁡(π3)=4⋅32=23\begin{aligned} x&=r\cos\theta=4\cos\left(\dfrac{\pi}{3}\right) =4\cdot\dfrac{1}{2}=2 \\ y&=r\sin\theta=4\sin\left(\dfrac{\pi}{3}\right) =4\cdot\dfrac{\sqrt{3}}{2}=2\sqrt{3} \end{aligned} So the point is (x,y)=(2,23)(x,y)=(2,2\sqrt{3}).

      js 

      [×]

    2. (r,θ)=(3,π2)(r,\theta)=\left(3,\dfrac{\pi}{2}\right)

      Hint

      What does θ=π2\theta=\dfrac{\pi}{2} mean?

      [×]

      Answer

      (x,y)=(0,3)(x,y)=(0,3)

      [×]

      Solution

      Since θ=π2\theta=\dfrac{\pi}{2}, the point lies on the positive yy-axis at a distance y=r=3y=r=3 from the origin. So the point is (x,y)=(0,3)(x,y)=(0,3). Of course the formulas would also work.

      js 

      [×]

    3. (r,θ)=(2,5π6)(r,\theta)=\left(2,\dfrac{5\pi}{6}\right)

      Hint

      The transformation equations from polar (r,θ)(r,\theta) to rectangular (x,y)(x,y), work in any quadrant. x=rcos⁡θy=rsin⁡θ x=r\cos\theta \qquad y=r\sin\theta

      [×]

      Answer

      (x,y)=(−3,1)(x,y)=(-\sqrt{3},1)

      [×]

      Solution

      Using r=2r=2 and θ=5π6\theta=\dfrac{5\pi}{6}, we compute x=rcos⁡θ=2cos⁡(5π6)=2⋅−32=−3y=rsin⁡θ=2sin⁡(5π6)=2⋅12=1\begin{aligned} x&=r\cos\theta=2\cos\left(\dfrac{5\pi}{6}\right) =2\cdot\dfrac{-\sqrt{3}}{2}=-\sqrt{3} \\ y&=r\sin\theta=2\sin\left(\dfrac{5\pi}{6}\right) =2\cdot\dfrac{1}{2}=1 \end{aligned} So the point is (x,y)=(−3,1)(x,y)=(-\sqrt{3},1).

      js 

      [×]

      Remark

      Notice that θ=5π6\theta=\dfrac{5\pi}{6} says the point is in quadrant II which agrees with the solution. The formulas work and there is nothing special to do for quadrants II and III.

      [×]

    3. b. Graphs of Polar Equations

    Graph the following polar equations:

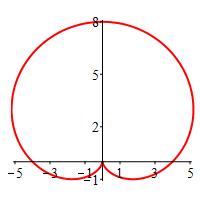
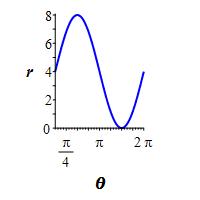
  3. r=4+4sin⁡θr=4+4\sin\theta

    Hint

    First graph a rectangular plot and use it to make the polar plot.

    [×]

    Answer

    r=4p4sinthetaP.jpg
    [×]

    Solution

    The rectangular plot is a sine curve stretched vertically by a factor of 44 and shifted up by 44. So it goes between 00 and 88.

    r=4p4sinthetaR.jpg

    A table of important values is:

    θ=\theta= 00 π2\dfrac{\pi}{2} π\pi 3π2\dfrac{3\pi}{2} 2π2 \pi
    r=r= 44 88 44 00 44

    So the polar plot starts at r=4r=4 when θ=0\theta=0, goes up to r=8r=8 when θ=π2\theta=\dfrac{\pi}{2}, falls back to r=4r=4 when θ=π\theta=\pi, falls to r=0r=0 when θ=3π2\theta=\dfrac{3\pi}{2}, and finally closes back to r=4r=4 when θ=2π\theta=2\pi.

    r=4p4sinthetaP.jpg

    js 

    [×]

  4. r=1+3cos⁡θr=1+3\cos\theta

    Answer

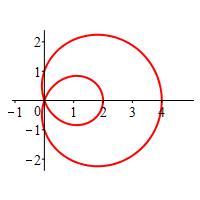
    r=1p3costhetaP.jpg
    [×]

    Solution

    The rectangular plot is a cosine curve stretched vertically by a factor of 33 and shifted up by 11. So it goes between −2-2 and 44.

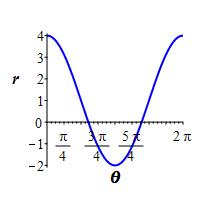
    r=1p3costhetaR.jpg

    To find where the graph passes through the origin, we solve r=1+3cos⁡θ=0r=1+3\cos\theta=0 to get θ=arccos⁡(−13)≈.6π \theta=\arccos\left(\dfrac{-1}{3}\right) \approx.6\pi which is a little more than π2\dfrac{\pi}{2}. A table of important values is:

    θ=\theta= 00 π2\dfrac{\pi}{2} .6π.6\pi π\pi 1.4π1.4\pi 3π2\dfrac{3\pi}{2} 2π2 \pi
    r=r= 44 11 00 −2-2 00 11 44

    So the polar plot starts at r=4r=4 when θ=0\theta=0, drops to r=1r=1 when θ=π2\theta=\dfrac{\pi}{2} and to r=0r=0 when θ=.6π\theta=.6\pi. Then it is negative which goes backwards until it reaches r=−2r=-2 at θ=π\theta=\pi. After that it is a mirror image.

    r=1p3costhetaP.jpg

    js 

    [×]

  5. r=2cos⁡2θr=2\cos2\theta

    Answer

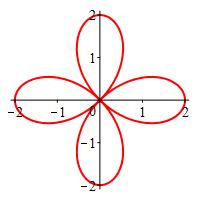
    r=2cos2thetaP.jpg
    [×]

    Solution

    The rectangular plot is a sine curve stretched vertically by a factor of 22 and compressed horizontally by a factor of 22.

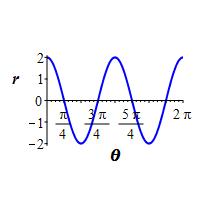
    r=2cos2thetaR.jpg

    To find where the graph passes through the origin, we solve r=2cos⁡2θ=0r=2\cos2\theta=0 to get θ=π4,3π4,5π4,7π4 \theta=\dfrac{\pi}{4},\dfrac{3\pi}{4},\dfrac{5\pi}{4},\dfrac{7\pi}{4} A table of important values is:

    θ=\theta= 00 π4\dfrac{\pi}{4} π2\dfrac{\pi}{2} 3π4\dfrac{3\pi}{4} π\pi 5π4\dfrac{5\pi}{4} 3π2\dfrac{3\pi}{2} 7π4\dfrac{7\pi}{4} 2π2\pi
    r=r= 22 00 −2-2 00 22 00 −2-2 00 22

    So the plot starts at r=2r=2 when θ=0\theta=0, falls to r=0r=0 when θ=π4\theta=\dfrac{\pi}{4}, goes backwards to r=−2r=-2 when θ=π2\theta=\dfrac{\pi}{2}, goes back to r=0r=0 when θ=3π4\theta=\dfrac{3\pi}{4}, and continues this pattern until it closes back to r=2r=2 when θ=2π\theta=2\pi.

    r=2cos2thetaP.jpg

    js 

    [×]

  6. r=2+2cos⁡2θr=2+2\cos2\theta

    Answer

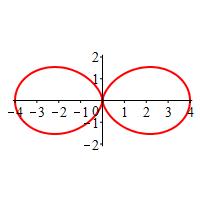
    r=2p2cos2thetaP.jpg
    [×]

    Solution

    The rectangular plot is a cosine curve stretched vertically by a factor of 22, compressed horizontally by a factor of 22, and shifted up by 22. So it goes between 00 and 44.

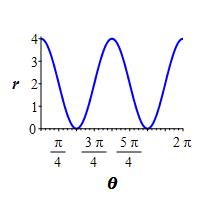
    r=2p2cos2thetaR.jpg

    A table of important values is:

    θ=\theta= 00 π2\dfrac{\pi}{2} π\pi 3π2\dfrac{3\pi}{2} 2π2\pi
    r=r= 44 00 44 00 44

    So the polar plot starts at r=4r=4 when θ=0\theta=0, falls to r=0r=0 when θ=π2\theta=\dfrac{\pi}{2}, goes back up to r=4r=4 when θ=π\theta=\pi, and has a mirror image back to θ=2π\theta=2\pi.

    r=2p2cos2thetaP.jpg

    js 

    [×]

  7. r=sin⁡4θr=\sin4\theta

    Answer

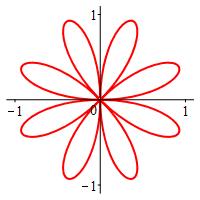
    r=sin4thetaP.jpg
    [×]

    Solution

    The rectangular plot is a sine curve compressed horizontally by a factor of 44.

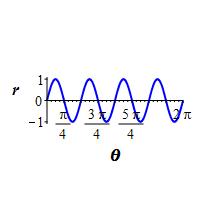
    r=sin4thetaR.jpg

    To find where the graph passes through the origin, we solve r=sin⁡4θ=0r=\sin4\theta=0. The zeros occurs when 4θ=kπ4\theta=k\pi. So: θ=kπ4fork=0,1,⋅,8 \theta=\dfrac{k\pi}{4} \quad \text{for} \quad k=0,1,\cdot,8

    Looking at the rectangular plot, we see there will be a positive loop between 00 and π4\dfrac{\pi}{4} which reaches r=1r=1, then a negative loop between π4\dfrac{\pi}{4} and π2\dfrac{\pi}{2}. These repeat 33 more times. It is important to notice that the negative loops never coincide with the positive loops. So we get an 88 leaf rose.

    r=sin4thetaP.jpg

    js 

    [×]

  8. r=2sin⁡5θr=2\sin5\theta

    Answer

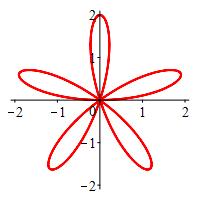
    r=2sin5thetaP.jpg
    [×]

    Solution

    The rectangular plot is a sine curve compressed horizontally by a factor of 55 and stretched vertically by a factor of 22.

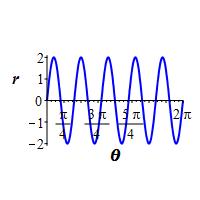
    r=2sin5thetaR.jpg

    To find where the graph passes through the origin, we solve r=sin⁡5θ=0r=\sin5\theta=0. The zeros occur when 5θ=kπ5\theta=k\pi. So: θ=kπ5fork=0,1,⋅,10 \theta=\dfrac{k\pi}{5} \quad \text{for} \quad k=0,1,\cdot,10

    Looking at the rectangular plot, we see there will be a positive loop between 00 and π5\dfrac{\pi}{5} which reaches r=2r=2, then a negative loop between π5\dfrac{\pi}{5} and 2π5\dfrac{2\pi}{5}. These repeat 44 more times. This seems to say there should be 1010 loops. However, looking at the polar plot, after θ=π\theta=\pi each loop overwrites one of the previous loops. For example, the loop between π\pi and 6π5\dfrac{6\pi}{5} is negative and overwrites the positive loop between 00 and 6π5\dfrac{6\pi}{5}. So we only get an 55 leaf rose.

    r=2sin5thetaP.jpg

    js 

    [×]

    9. c. Slope of a Polar Graph

  9. Find the slope of the function r=2cos⁡θr=2\cos\theta for the following values of θ\theta:

    1. θ=π6\theta=\dfrac{\pi}{6}

      Hint

      Given a polar function r(θ)r(\theta), the slope of that function at a given value of θ\theta is dydx=r′(θ)sin⁡θ+r(θ)cos⁡θr′(θ)cos⁡θ−r(θ)sin⁡θ \dfrac{dy}{dx}=\dfrac{r'(\theta)\sin\theta+r(\theta)\cos\theta} {r'(\theta)\cos\theta-r(\theta)\sin\theta }

      [×]

      Answer

      dydx=−13\dfrac{dy}{dx}=-\,\dfrac{1}{\sqrt{3}}

      [×]

      Solution

      Given r(θ)=2cos⁡θr(\theta)=2\cos\theta, the derivative is r′=−2sin⁡θr'=-2\sin\theta. We have: sin⁡(π6)=12cos⁡(π6)=32r(π6)=3r′(π6)=−1\begin{aligned} \sin\left(\dfrac{\pi}{6}\right)&=\dfrac{1}{2} &\qquad \cos\left(\dfrac{\pi}{6}\right)&=\dfrac{\sqrt{3}}{2} \\[6pt] r\left(\dfrac{\pi}{6}\right)&=\sqrt{3} &\qquad r'\left(\dfrac{\pi}{6}\right)&=-1 \end{aligned} So: dydx∣π/6=r′(θ)sin⁡θ+r(θ)cos⁡θr′(θ)cos⁡θ−r(θ)sin⁡θ=−1(12)+3(32)−1(32)−3(12)=−1+3−3−3=−13\begin{aligned} \left.\dfrac{dy}{dx}\right|_{\pi/6} &=\dfrac{r'(\theta)\sin\theta+r(\theta)\cos\theta} {r'(\theta)\cos\theta-r(\theta)\sin\theta }\\ &=\dfrac{-1\left(\dfrac{1}{2}\right)+\sqrt{3}\left(\dfrac{\sqrt{3}}{2}\right)} {-1\left(\dfrac{\sqrt{3}}{2}\right)-\sqrt{3}\left(\dfrac{1}{2}\right)} \\ &=\dfrac{-1+3}{-\sqrt{3}-\sqrt{3}} =-\,\dfrac{1}{\sqrt{3}} \end{aligned}

      js 

      [×]

    2. θ=π4\theta=\dfrac{\pi}{4}

      Answer

      dydx=0\dfrac{dy}{dx}=0

      [×]

      Solution

      Given r(θ)=2cos⁡θr(\theta)=2\cos\theta, the derivative is r′=−2sin⁡θr'=-2\sin\theta. We have: sin⁡(π4)=12cos⁡(π4)=12r(π4)=2r′(π4)=−2\begin{aligned} \sin\left(\dfrac{\pi}{4}\right)&=\dfrac{1}{\sqrt{2}} &\qquad \cos\left(\dfrac{\pi}{4}\right)&=\dfrac{1}{\sqrt{2}} \\ r\left(\dfrac{\pi}{4}\right)&=\sqrt{2} &\qquad r'\left(\dfrac{\pi}{4}\right)&=-\sqrt{2} \end{aligned} So: dydx∣π/4=r′(θ)sin⁡θ+r(θ)cos⁡θr′(θ)cos⁡θ−r(θ)sin⁡θ=−2(12)+2(12)−2(12)−2(12)=−1+1−1−1=0−2=0\begin{aligned} \left.\dfrac{dy}{dx}\right|_{\pi/4}&=\dfrac{r'(\theta)\sin\theta+r(\theta)\cos\theta} {r'(\theta)\cos\theta-r(\theta)\sin\theta }\\ &=\dfrac{-\sqrt{2}\left(\dfrac{1}{\sqrt{2}}\right) +\sqrt{2}\left(\dfrac{1}{\sqrt{2}}\right)} {-\sqrt{2}\left(\dfrac{1}{\sqrt{2}}\right) -\sqrt{2}\left(\dfrac{1}{\sqrt{2}}\right)} \\ &=\dfrac{-1+1}{-1-1}=\dfrac{0}{-2}=0 \end{aligned}

      js 

      [×]

    3. θ=13π6\theta=\dfrac{13\pi}{6}

      Answer

      dydx=−13\dfrac{dy}{dx}=-\,\dfrac{1}{\sqrt{3}}

      [×]

      Solution

      Given r(θ)=2cos⁡θr(\theta)=2\cos\theta, the derivative is r′=−2sin⁡θr'=-2\sin\theta. So: sin⁡(13π6)=12cos⁡(13π6)=32r(13π6)=3r′(13π6)=−1\begin{aligned} \sin\left(\dfrac{13\pi}{6}\right)&=\dfrac{1}{2} &\qquad \cos\left(\dfrac{13\pi}{6}\right)&=\dfrac{\sqrt{3}}{2} \\[6pt] r\left(\dfrac{13\pi}{6}\right)&=\sqrt{3} &\qquad r'\left(\dfrac{13\pi}{6}\right)&=-1 \end{aligned} So: dydx∣13π/6=r′(θ)sin⁡θ+r(θ)cos⁡θr′(θ)cos⁡θ−r(θ)sin⁡θ=−1(12)+3(32)−1(32)−3(12)=−1+3−3−3=−13\begin{aligned} \left.\dfrac{dy}{dx}\right|_{13\pi/6} &=\dfrac{r'(\theta)\sin\theta+r(\theta)\cos\theta} {r'(\theta)\cos\theta-r(\theta)\sin\theta }\\ &=\dfrac{-1\left(\dfrac{1}{2}\right)+\sqrt{3}\left(\dfrac{\sqrt{3}}{2}\right)} {-1\left(\dfrac{\sqrt{3}}{2}\right)-\sqrt{3}\left(\dfrac{1}{2}\right)} \\ &=\dfrac{-1+3}{-\sqrt{3}-\sqrt{3}} =-\,\dfrac{1}{\sqrt{3}} \end{aligned}

      js 

      [×]

      Remark

      The fact that parts (a) and (c) have the same answer should be no suprise! The period of 2cos⁡θ2\cos\theta is 2π2\pi. So θ=13π6=2π+π6\theta=\dfrac{13\pi}{6}=2\pi+\dfrac{\pi}{6} gives the same answer as θ=π6\theta=\dfrac{\pi}{6}.

      [×]
  10. Find the slope of the function r=1+2sin⁡θr=1+2\sin\theta for the following values of θ\theta:

    1. θ=−π4\theta=-\,\dfrac{\pi}{4}

      Hint

      Given a polar function r(θ)r(\theta), the slope of that function at a given value of θ\theta is dydx=r′(θ)sin⁡θ+r(θ)cos⁡θr′(θ)cos⁡θ−r(θ)sin⁡θ \dfrac{dy}{dx}=\dfrac{r'(\theta)\sin\theta+r(\theta)\cos\theta} {r'(\theta)\cos\theta-r(\theta)\sin\theta }

      [×]

      Answer

      dydx=1−22\dfrac{dy}{dx}=1-2\sqrt{2}

      [×]

      Solution

      Given r(θ)=1+2sin⁡θr(\theta)=1+2\sin\theta, the derivative is r′=2cos⁡θr'=2\cos\theta. We know: sin⁡(−π4)=−12cos⁡(−π4)=12r(−π4)=1−2r′(−π4)=2\begin{aligned} \sin\left(-\,\dfrac{\pi}{4}\right)&=-\,\dfrac{1}{\sqrt{2}} &\qquad \cos\left(-\,\dfrac{\pi}{4}\right)&=\dfrac{1}{\sqrt{2}} \\ r\left(-\,\dfrac{\pi}{4}\right)&=1-\sqrt{2} &\qquad r'\left(-\,\dfrac{\pi}{4}\right)&=\sqrt{2} \end{aligned} So: dydx∣−π/4=r′(θ)sin⁡θ+r(θ)cos⁡θr′(θ)cos⁡θ−r(θ)sin⁡θ=2(−12)+(1−2)(12)2(12)−(1−2)(−12)=−1+12−11+12−1=12−212=1−22\begin{aligned} \left.\dfrac{dy}{dx}\right|_{-\pi/4}&=\dfrac{r'(\theta)\sin\theta+r(\theta)\cos\theta} {r'(\theta)\cos\theta-r(\theta)\sin\theta }\\ &=\dfrac{\sqrt{2}\left(-\,\dfrac{1}{\sqrt{2}}\right) +(1-\sqrt{2})\left(\dfrac{1}{\sqrt{2}}\right)} {\sqrt{2}\left(\dfrac{1}{\sqrt{2}}\right) -(1-\sqrt{2})\left(-\,\dfrac{1}{\sqrt{2}}\right)} \\ &=\dfrac{-1+\dfrac{1}{\sqrt{2}}-1} {1+\dfrac{1}{\sqrt{2}}-1} \\ &=\dfrac{\dfrac{1}{\sqrt{2}}-2}{\dfrac{1}{\sqrt{2}}}=1-2\sqrt{2} \end{aligned}

      js 

      [×]

    2. θ=11π6\theta=\dfrac{11\pi}{6}

      Answer

      dydx=−13\dfrac{dy}{dx}=-\,\dfrac{1}{\sqrt{3}}

      [×]

      Solution

      Given r(θ)=1+2sin⁡θr(\theta)=1+2\sin\theta, the derivative is r′=2cos⁡θr'=2\cos\theta. We have: sin⁡(11π6)=−12cos⁡(11π6)=32r(11π6)=0r′(11π6)=3\begin{aligned} \sin\left(\dfrac{11\pi}{6}\right)&=-\,\dfrac{1}{2} &\qquad \cos\left(\dfrac{11\pi}{6}\right)&=\dfrac{\sqrt{3}}{2} \\[6pt] r\left(\dfrac{11\pi}{6}\right)&=0 &\qquad r'\left(\dfrac{11\pi}{6}\right)&=\sqrt{3} \end{aligned} So: dydx∣11π/6=r′(θ)sin⁡θ+r(θ)cos⁡θr′(θ)cos⁡θ−r(θ)sin⁡θ=3(−12)+(0)(32)3(32)−(0)(−12)=−33=−13\begin{aligned} \left.\dfrac{dy}{dx}\right|_{11\pi/6} &=\dfrac{r'(\theta)\sin\theta+r(\theta)\cos\theta} {r'(\theta)\cos\theta-r(\theta)\sin\theta }\\ &=\dfrac{\sqrt{3} \left(-\,\dfrac{1}{2} \right) +(0)\left(\dfrac{\sqrt{3}}{2}\right)} {\sqrt{3}\left(\dfrac{\sqrt{3}}{2}\right) -(0)\left(-\,\dfrac{1}{2}\right)} \\ &=\dfrac{-\sqrt{3}}{3} =-\,\dfrac{1}{\sqrt{3}} \end{aligned}

      [×]

      Remark

      This is a special case where r(θ)=0r(\theta)=0. So the formula reduces to: dydx=r′(θ)sin⁡θ+r(θ)cos⁡θr′(θ)cos⁡θ−r(θ)sin⁡θ=sin⁡θcos⁡θ=tan⁡θ\begin{aligned} \dfrac{dy}{dx} &=\dfrac{r'(\theta)\sin\theta+r(\theta)\cos\theta} {r'(\theta)\cos\theta-r(\theta)\sin\theta} \\ &=\dfrac{\sin\theta}{\cos\theta}=\tan\theta \end{aligned} and dydx=tan⁡(11π6)=−13\dfrac{dy}{dx}=\tan\left(\dfrac{11\pi}{6}\right) =-\,\dfrac{1}{\sqrt{3}}.

      js 

      [×]

    3. θ=π\theta=\pi

      Answer

      dydx=−12\dfrac{dy}{dx}=-\,\dfrac{1}{2}

      [×]

      Solution

      Given r(θ)=1+2sin⁡θr(\theta)=1+2\sin\theta, the derivative is r′=2cos⁡θr'=2\cos\theta. We have: sin⁡(π)=0cos⁡(π)=−1r(π)=1r′(π)=−2\begin{aligned} \sin(\pi)&=0 &\qquad \cos(\pi)&=-1 \\ r(\pi)&=1 &\qquad r'(\pi)&=-2 \end{aligned} So: dydx∣π=r′(θ)sin⁡θ+r(θ)cos⁡θr′(θ)cos⁡θ−r(θ)sin⁡θ=−2(0)+1(−1)−2(−1)−1(0)=−12\begin{aligned} \left.\dfrac{dy}{dx}\right|_\pi &=\dfrac{r'(\theta)\sin\theta+r(\theta)\cos\theta} {r'(\theta)\cos\theta-r(\theta)\sin\theta }\\ &=\dfrac{-2(0) +1(-1)} {-2(-1) -1(0)} =-\,\dfrac{1}{2} \end{aligned}

      js 

      [×]

    11. d. Area Enclosed by a Polar Graph

    Find the area enclosed by each curve:

  11. r=2cos⁡θr=2\cos\theta

    Hint

    The area of a polar region bounded by the function r(θ)r(\theta) and spanning from θ=α\theta=\alpha to θ=β\theta=\beta is A=∫αβ12(r(θ))2dθ A=\int_\alpha^\beta \dfrac{1}{2}(r(\theta))^2\,d\theta

    [×]

    Answer

    A=πA=\pi

    [×]

    Solution

    Looking at the plot, we see we need to integrate between θ=−π2\theta=-\,\dfrac{\pi}{2} and θ=π2\theta=\dfrac{\pi}{2}.

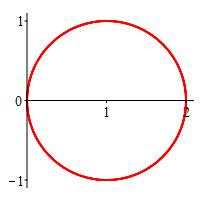
    r=2costhetaF.jpg

    We thus compute:

    A=∫αβ12(r(θ))2dθ=∫0π12(2cos⁡θ)2dθ=2∫0πcos⁡2θdθ\begin{aligned} A&=\int_\alpha^\beta \dfrac{1}{2}(r(\theta))^2\,d\theta \\ &=\int_0^\pi \dfrac{1}{2}(2\cos\theta)^2\,d\theta \\ &=2\int_0^\pi \cos^2\theta\,d\theta \\ \end{aligned}

    We then apply the trig identity cos⁡2θ=1+cos⁡2θ2\cos^2\theta=\dfrac{1+\cos2\theta}{2}:

    A=2∫0π1+cos⁡2θ2dθ=[θ+sin⁡2θ2]0π=(π+0)−(0+0)=π\begin{aligned} A&=2\int_0^\pi \dfrac{1+\cos2\theta}{2}\,d\theta \\ &=\left[\theta+\dfrac{\sin2\theta}{2} \right]_0^\pi \\ &=(\pi+0)-(0+0) \\ &=\pi \end{aligned}

    js 

    [×]

    Answer

    Without doing any calculus, we should have know the answer immediately as r=2cos⁡θr=2\cos\theta is a circle centered at (1,0)(1,0) with radius 11.

    [×]

  12. One leaf of the rose r=3sin⁡2θr=3\sin2\theta.

    Hint

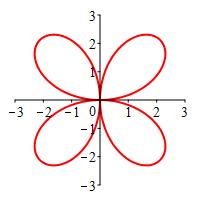
    r=3sin2theta.jpg
    [×]

    Answer

    A=9π8A=\dfrac{9\pi}{8}

    [×]

    Solution

    Looking at the plot, we see this is a 44-leaf rose. The radius goes to 00 when 2θ=kπ2\theta=k\pi or θ=kπ2\theta=k\dfrac{\pi}{2}. We can pick any leaf but the obvious one is 0≤θ≤π20 \le \theta \le \dfrac{\pi}{2}.

    r=3sin2theta.jpg

    We thus compute: A=∫αβ12(r(θ))2dθ=∫0π/212(3sin⁡2θ)2dθ=92∫0π/2sin⁡22θdθ\begin{aligned} A&=\int_\alpha^\beta \dfrac{1}{2}(r(\theta))^2\,d\theta \\ &=\int_0^{\pi/2} \dfrac{1}{2}(3\sin2\theta)^2\,d\theta \\ &=\dfrac{9}{2}\int_0^{\pi/2} \sin^2 2\theta\,d\theta \\ \end{aligned}

    We then apply the trig identity sin⁡2θ=1−cos⁡2θ2\sin^2\theta=\dfrac{1-\cos2\theta}{2}: A=94∫0π/21−cos⁡4θdθ=94[θ−sin⁡4θ4]0π/2=94[(π2+0)−(0+0)]=9π8\begin{aligned} A&=\dfrac{9}{4}\int_0^{\pi/2} 1-\cos4\theta\,d\theta \\ &=\dfrac{9}{4}\left[\theta-\dfrac{\sin4\theta}{4} \right]_0^{\pi/2} \\ &=\dfrac{9}{4}\left[\left(\dfrac{\pi}{2}+0\right)-(0+0)\right] \\ &=\dfrac{9\pi}{8} \end{aligned}

    js 

    [×]

  13. One petal of the flower r=2+2sin⁡3θr=2+2\sin3\theta.

    Hint

    You first need to find when r=0r=0.

    [×]

    Answer

    A=2πA=2\pi

    [×]

    Solution

    We first need to know when r=0r=0. So we solve: r=2+2sin⁡3θ=02sin⁡3θ=−2sin⁡3θ=−13θ=−π2+2πkθ=−π6+2π3kθ=−π+4πk6\begin{aligned} r=2+2\sin3\theta&=0 \\ 2\sin3\theta&=-2 \\ \sin3\theta&=-1 \\ 3\theta&=-\,\dfrac{\pi}{2}+2\pi k \\ \theta&=-\,\dfrac{\pi}{6}+\dfrac{2\pi}{3} k \\ \theta&=\dfrac{-\pi+4\pi k}{6} \\ \end{aligned}

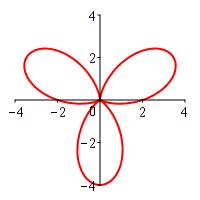
    r=2p2sin3theta.jpg

    For 0≤θ≤2π0 \le \theta \le 2\pi this gives us r=0r=0 when θ=π2,7π6,11π6\theta=\dfrac{\pi}{2},\dfrac{7\pi}{6},\dfrac{11\pi}{6}. We take 22 consecutive values of θ\theta as our interval of integration and compute: A=∫π/27π/612(r(θ))2dθ=∫π/27π/612(2+2sin⁡3θ)2dθ=12∫π/27π/64+8sin⁡3θ+4sin⁡23θdθ=∫π/27π/62+4sin⁡3θ+2sin⁡23θdθ\begin{aligned} A&=\int_{\pi/2}^{7\pi/6} \dfrac{1}{2}(r(\theta))^2\,d\theta \\ &=\int_{\pi/2}^{7\pi/6} \dfrac{1}{2}(2+2\sin3\theta)^2\,d\theta \\ &=\dfrac{1}{2}\int_{\pi/2}^{7\pi/6} 4+8\sin3\theta+4\sin^2 3\theta \,d\theta \\ &=\int_{\pi/2}^{7\pi/6} 2+4\sin3\theta+2\sin^2 3\theta \,d\theta \\ \end{aligned} We then apply the trig identity sin⁡2θ=1−cos⁡2θ2\sin^2\theta=\dfrac{1-\cos2\theta}{2}: A=∫π/27π/62+4sin⁡3θ+(1−cos⁡6θ)dθ=∫π/27π/63+4sin⁡3θ−cos⁡6θdθ=[3θ−43cos⁡3θ−16sin⁡6θ]π/27π/6=[(7π2−0−0)−(3π2−0−0)]=4π2=2π\begin{aligned} A&=\int_{\pi/2}^{7\pi/6} 2+4\sin3\theta+(1-\cos6\theta)\,d\theta \\ &=\int_{\pi/2}^{7\pi/6} 3+4\sin3\theta -\cos6\theta \,d\theta \\ &=\left[3\theta -\dfrac{4}{3}\cos3\theta -\dfrac{1}{6}\sin6\theta \right]_{\pi/2}^{7\pi/6} \\ &=\left[(\dfrac{7\pi}{2}-0-0)-(\dfrac{3\pi}{2}-0-0)\right]\\ &=\dfrac{4\pi}{2}=2\pi \end{aligned}

    js 

    [×]

    14. e. Arc Length of a Polar Graph

    Find the arc length of each curve on the indicated interval.

  14. r=cos⁡θ+sin⁡θr=\cos\theta+\sin\theta over the inteval [0,π][0,\pi]

    Hint

    The arc length of a polar curve r=r(θ)r=r(\theta) from θ=α\theta=\alpha to θ=β\theta=\beta is L=∫αβr(θ)2+(drdθ)2dθ L=\int_\alpha^\beta \sqrt{\,r(\theta)^2+\left(\dfrac{dr}{d\theta}\right)^2}\,d\theta

    [×]

    Answer

    L=2πL=\sqrt{2}\,\pi

    [×]

    Solution

    We compute L=∫αβr(θ)2+(drdθ)2dθ=∫0π(cos⁡θ+sin⁡θ)2+(−sin⁡θ+cos⁡θ)2dθ=∫0π(cos⁡2θ+2cos⁡θsin⁡θ+sin⁡2θ)+(sin⁡2θ−2sin⁡θcos⁡θ+cos⁡2θ)dθ=∫0π2cos⁡2θ+2sin⁡2θdθ=∫0π2dθ=2θ∣0π=2π\begin{aligned} L&=\int_\alpha^\beta \sqrt{ r(\theta)^2+\left(\dfrac{dr}{d\theta}\right)^2 }\,d\theta \\ &=\int_0^\pi \sqrt{(\cos\theta+\sin\theta)^2 +(-\sin\theta+\cos\theta)^2}\,d\theta \\ &=\int_0^\pi \sqrt{ (\cos^2\theta+2\cos\theta\sin\theta+\sin^2\theta) +(\sin^2\theta-2\sin\theta\cos\theta+\cos^2\theta)}\,d\theta \\ &=\int_0^\pi \sqrt{2\cos^2\theta+2\sin^2\theta}\,d\theta \\ &=\int_0^\pi \sqrt{2}\,d\theta =\left.\sqrt{2}\,\theta\rule{0pt}{10pt}\right|_0^\pi =\sqrt{2}\,\pi \end{aligned}

    js 

    [×]

  15. r=sin⁡2θ2r=\sin^2\dfrac{\theta}{2} over the interval [0,π][0,\pi]

    Answer

    L=2L=2

    [×]

    Solution

    We compute L=∫αβr(θ)2+(drdθ)2dθ=∫0π(sin⁡2(θ2))2+(sin⁡(θ2)cos⁡(θ2))2dθ=∫0πsin⁡4(θ2)+sin⁡2(θ2)cos⁡2(θ2)dθ=∫0πsin⁡2(θ2)(sin⁡2(θ2)+cos⁡2(θ2))dθ=∫0πsin⁡2(θ2)dθ=∫0π∣sin⁡(θ2)∣dθ\begin{aligned} L&=\int_\alpha^\beta \sqrt{ r(\theta)^2+\left(\dfrac{dr}{d\theta}\right)^2}\,d\theta \\ &=\int_0^\pi \sqrt{ \left(\sin^2\left(\dfrac{\theta}{2}\right)\right)^2 +\left(\sin\left(\dfrac{\theta}{2}\right)\cos\left(\dfrac{\theta}{2}\right)\right)^2 }\,d\theta \\ &=\int_0^\pi \sqrt{ \sin^4\left(\dfrac{\theta}{2}\right) +\sin^2\left(\dfrac{\theta}{2}\right)\cos^2\left(\dfrac{\theta}{2}\right) }\,d\theta \\ &=\int_0^\pi \sqrt{ \sin^2\left(\dfrac{\theta}{2}\right) \left( \sin^2\left(\dfrac{\theta}{2}\right)+\cos^2\left(\dfrac{\theta}{2}\right) \right) }\,d\theta \\ &=\int_0^\pi \sqrt{ \sin^2\left(\dfrac{\theta}{2}\right) }\,d\theta \\ &=\int_0^\pi \left|\sin\left(\dfrac{\theta}{2}\right)\right| \,d\theta \end{aligned} Since sin⁡(θ2)≥0\sin\left(\dfrac{\theta}{2}\right) \ge 0 on the interval [0,π][0,\pi], we can get rid of the absolute value: L=∫0πsin⁡(θ2)dθ=[−2cos⁡(θ2)]0π=[−2(0)−(−2(1))]=2\begin{aligned} L&=\int_0^\pi \sin\left(\dfrac{\theta}{2}\right)\,d\theta \\ &=\left[-2\cos\left(\dfrac{\theta}{2}\right)\right]_0^\pi \\ &=[-2(0)-(-2(1))] =2 \end{aligned}

    js 

    [×]

  16. r=sec⁡θr=\sec\theta over the interval [−π4,π4]\left[-\,\dfrac{\pi}{4},\dfrac{\pi}{4}\right]

    Answer

    L=2L=2

    [×]

    Solution

    We compute: L=∫αβr(θ)2+(drdθ)2dθ=∫−π/4π/4(sec⁡θ)2+(sec⁡θtan⁡θ)2dθ=∫−π/4π/4sec⁡2θ+sec⁡2θtan⁡2θdθ=∫−π/4π/4sec⁡2θ(1+tan⁡2θ)dθ=∫−π/4π/4sec⁡4θdθ=∫−π/4π/4sec⁡2θdθ=tan⁡θ∣−π/4π/4=1−(−1)=2\begin{aligned} L&=\int_\alpha^\beta \sqrt{r(\theta)^2+\left(\dfrac{dr}{d\theta}\right)^2}\,d\theta \\ &=\int_{-\pi/4}^{\pi/4} \sqrt{(\sec\theta)^2+(\sec\theta\tan\theta)^2}\,d\theta \\ &=\int_{-\pi/4}^{\pi/4} \sqrt{\sec^2\theta+\sec^2\theta\tan^2\theta}\,d\theta \\ &=\int_{-\pi/4}^{\pi/4} \sqrt{\sec^2\theta(1+\tan^2\theta)}\,d\theta \\ &=\int_{-\pi/4}^{\pi/4} \sqrt{\sec^4\theta}\,d\theta =\int_{-\pi/4}^{\pi/4} \sec^2\theta\,d\theta \\ &=\left.\tan\theta\rule{0pt}{10pt}\right|_{-\pi/4}^{\pi/4} =1-(-1)=2 \end{aligned}

    js 

    [×]
    17. PY: Checked to here.

    Review Exercises

  17. xxx

    Hint

    xxx

    [×]

    Answer

    xxx

    [×]

    Solution

    xxx

    [×]

  18. xxx

    Hint

    xxx

    [×]

    Answer

    xxx

    [×]

    Solution

    xxx

    [×]

© 2025 MYMathApps

Supported in part by NSF Grant #1123255